旧衣服的50种用途（旧衣服的利用用途）

是否勾住了你的心？漂亮的刺绣服饰，刺绣针法很简单

是不是你也有这种感觉，整理衣橱是个令人头疼又头大的难题，明明衣服塞得满柜子都是，却常常感到没有什么衣服穿。好多衣服都是九成新以上旧衣服的50种用途，弃之可惜，穿之嫌弃，越整理越心烦……

其实有些质地比较好、但是款式略微过时的服装，我们可以在上面绣一点儿好看的刺绣图案，旧衣立马就变成新衣服了。

刺绣针法万变不离其宗，只要学会那些基础针法，举一反三，就可以绣出很多很多种刺绣图案了。

普普通通的小包包，只要在上面绣上一些花花草草，就变得与众不同了。

普普通通的条纹小衫，领口上绣些美丽的花卉图案，立马就变得更加漂亮别致了。

牛仔背心原本比较硬朗的线条，因为绣上了简单的刺绣图案，立马就变得柔美了~~

这里再次分享21种刺绣针法图解教程，学会这21种，就能玩转刺绣哦！

喜欢刺绣却不知道从何下手

你可以试着先从基础的针法学起

掌握好基础后才能练就“大虾”

第一种：倒针绣

从1上，2下，3上，然后回到1把针带到后面

第二种：回针网格绣

适合用来填充某个区域

先缝一组平行线

然后再倒着十字交叉缝另一组平行线

整个刺绣过程需要保证针距一致

第三种：锁边绣

用途很广

常被用于贴布边缘的装饰绣，以及真正的锁边功能

第四种：卷针绣

卷针绣（也称绕针绣或缠针绣）

常被用来绣玫瑰或蔷薇

第五种：链针绣

链针绣的刺绣方向是从右到左

第一针出针后，线甩到左边，在紧邻出针位入针，向左穿越一定的针距后出针后收线，形成第一个链环，继而在出针处旁边入针，开始又一轮的循环。

第六种：殖民结

殖民结有点像用针线绕出一个“8”

然后从中间穿过布料固定出一个结

如果你很贴近的看这个结也很像一个数字“8”

第七种：法国结

把线在针上绕几圈，然后从中间穿过布料固定出一个结，看上去像一个玫瑰花朵，优点是可以做出你所需要的大小的结，需要大的结就多绕几圈线。

第八种：飞针绣

这是汉族刺绣基本针法之一，主要运用于蜀绣，是一种长短不一的乱针脚，在运针上有的两针相逗，有的用E3针，是一种适用于浸色的补充针法，而能掩藏原针层的埂子。

第九种：藏针缝

藏针缝就是藏匿线迹的缝法

藏针缝有很多种，比如立针、对针、梯子针等。

第十种：菊叶绣

通常用于绣花瓣

在1点上来，然后回到第1点，留下一个小循环，通过2点的循环，然后在第3点向下。

（旁边的点2，但不是相同的孔）

第十一种：立体叶子绣

一般用来刺绣立体的花，叶，羽毛和其他你需要的刺绣效果，底座是固定在布料上的，但其余的针脚是在空中。

将一个珠针垂直穿过布料，把针上升到1点，把针线穿过布料，然后回到2点，再回到3点旁边的针和中心1和2之间的点，把针线根据三个垂直线迹推到顶端，然后把针线通过上方，下方，在垂直线迹里重复，来回刺绣，保证每次的线迹平滑均匀。

第十二种：雌蕊绣

与法国结类似

这种针法类似于花的中心，在1点上来，然后把针绕两次，把针穿过2点，将线拉紧，靠近针，靠近布料，然后慢慢拉紧打结。

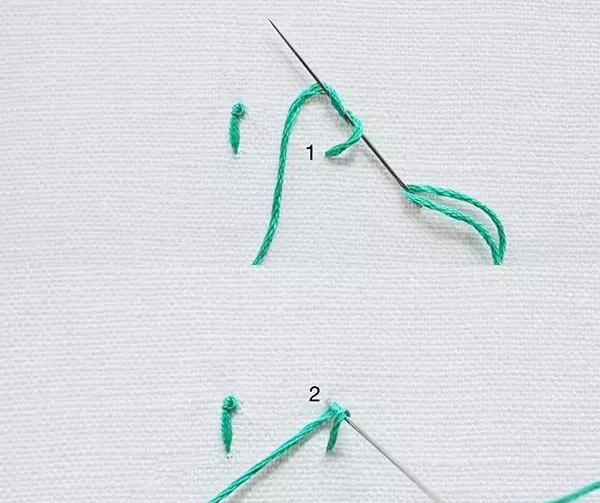
第十三种：玫瑰绣

用三个小平行缝形成一个中心，使用中心周围的茎缝，增加圈数，直到玫瑰达到所需的大小。

第十四种： 缎面绣

同样是用于填补区域，最好是在小的区域。

在1点上来，然后在第2点走下去，在3点上来，然后在第4点走下去，重复……

第十五种：扇贝绣

类似于雏菊，可以用来绣笑脸

在1点上来，然后在第2点往下走，把线松开，在3点上来，可拿起绣线循环，然后在第4点。

（旁边的点3，但不是相同的孔）

第十六种：劈针绣

具体绣法：第二针倒回从第一针中穿出，把第一针劈成两半，完成后形成辫子形状。

=第十七种：茎绣

常被用来绣茎干、轮廓线等

具体绣法是从后面1点上来，然后在第2点走下去。在将针脚贴近布料之前，用针下面的松螺纹向3点走拉紧螺纹，然后重复，从后面1点上来，然后在第2点走下去，在将针脚贴近布料之前，用针下面的松螺纹向3点走，拉紧螺纹，然后重复

第十八种：直针

最简单也是最基础的针法

1上2下的重复旧衣服的50种用途，但直针用的好，作品也很漂亮，之前提到的长短针就是用的直针针法。

第十九种：绕线回针绣

看上去像是在平针绣上绕线，先在布上绣上回针绣作为基础，从一个线的针到1点上来，滑针第一针从上下下来，将针从下一个针脚向下滑动重复，结束时把针放在点2。

第二十种：蛛网绣

这个针法看起来简单，实际也很简单，而且绣出的花也很漂亮，先打叉，然后再打叉，变成八条

在没有穿过织物的情况下，将针滑到辐条1和2下面，将针放在辐条2上，然后将针滑到辐条2和3下面，围绕所有辐条连续几次，直到填充完毕。

第二十一种：蛛网玫瑰绣

它的辐条可以根据需要而定，但需要保持奇数数量。

绣法：把针靠近轮子的中心，把针递过一个辐条拉线，重复。将针在轮子的辐条上方和下方编织轮子满时针扎到背后即可。

针法教程非常的详细，一定要学起来哦！